The 60:1 Rule and related derivations
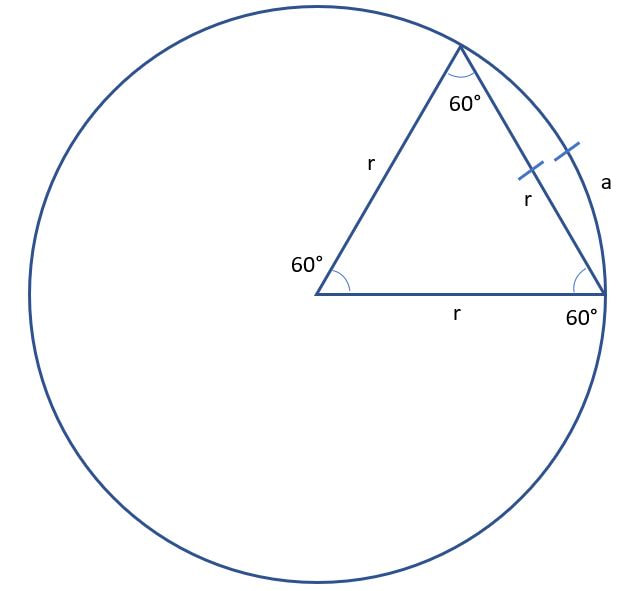
At some point you've probably run into the 60:1 rule and wondered how it came to be and what all we can do with it. At its core, the 60:1 rule uses two simple geometric approximations to give us a host of valuable derivations to fly with. To start, grab a piece of paper and sketch out an equilateral triangle. Label each internal angle with 60 degrees, and each edge with the letter "r." Next, draw a circle that's centered on one corner of the triangle that touches the other corners and has the same radius r. Label the arc between the vertices "a." It should look something like this:
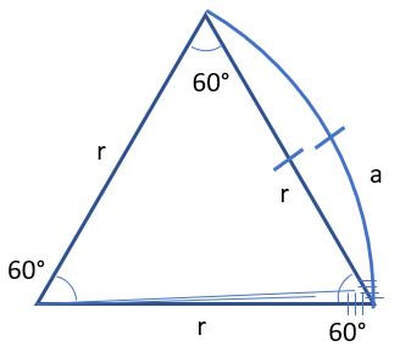
You'll notice that arc a and length r are almost the same length. If you remember back to geometry class, the circumference of a circle is 2πr, and that π≈3.14. Thus, 2πr≈6.28r. If you stack 6 triangles in the circle (6 * 60 = 360 degrees), and each has edge length r, then the circumference of the resulting hexagon is 6r. Thus, the relationship between the circle and hexagon is 6.28r/6r=1.0467. In other words, the length of the arc a is within 5% of the length of r. This means that for small angles where we plan to round to the nearest degree, a 5% error is trivial. That's our first little approximation. Next, we want to look at what happens when we chop length r and arc a into small chunks. Let's say we chop each length up into 60 chunks radially from the opposite corners. Realistically, we could chop each r or a into any n chunks, but let's use n=60 because we use degrees when we fly (if we navigated by radians, the same r≈a approximation would apply, and we'd just call it "the rule of 1."). Blame the Babylonians for the 60 degrees. Ok, so now each face of our triangle is divided into 60 roughly equal chunks. I've sketched out the bottom right corner and left the rest open for de-cluttering:
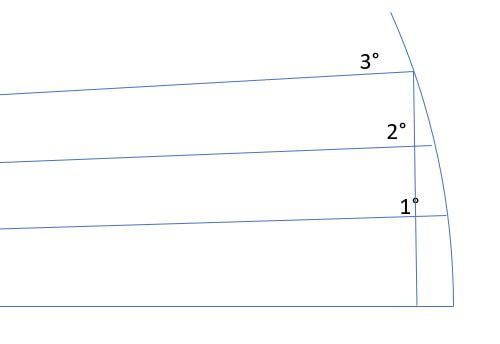
One relationship that jumps right out at us is that if r≈a, then for each degree, we have r/60 units of length on the opposite edge or arc. In other words, for every degree of deflection, we have 1/60th of r as distance displaced from the bottom line. So if r is 60 nm, then a degree puts us a mile off course. Our second hand-wave approximation, closely related to the first, is that the length of an arc opposite angle θ and the height of a right triangle with angle θ are the same. Let's zoom in on that bottom right corner of the arc that we chopped into 60 pieces:
Looking at that 3-degree slice, we can approximate the height of the vertical line forming the right triangle as the arc length around the outside. Combining that with our earlier discovery, we can say that a gradient of θ degrees gives us θ units of vertical displacement for every 60 units of lateral displacement. In other words, tan(θ)=θ/60. For those engineers and trigonometricians out there screaming foul, tan(1)=.017455, and 1/60 is .016667. That's still only 4.73% off. Close enough for us pilots.
One useful coincidence for us is that a nautical mile is 6076 feet. 6076≈6000 (within 1.3%).
1/60 = 100/6000 = 100 feet/nm
Combine that with our earlier findings, we derive that a gradient or glide path angle of θ degrees gives θ * 100 ft/nm.
Now let's look at what we can do with these relationships.
One useful coincidence for us is that a nautical mile is 6076 feet. 6076≈6000 (within 1.3%).
1/60 = 100/6000 = 100 feet/nm
Combine that with our earlier findings, we derive that a gradient or glide path angle of θ degrees gives θ * 100 ft/nm.
Now let's look at what we can do with these relationships.
Wind correction angles
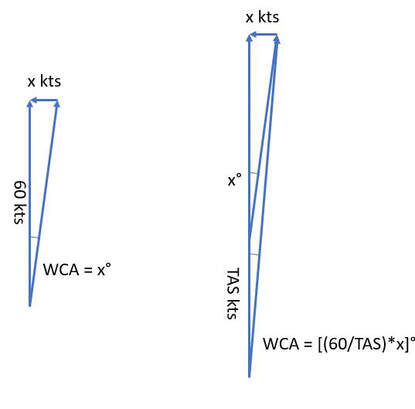
Let's say we have a crosswind component of x knots. That means that in every hour, the wind pushes us x nm sideways. If our speed is 60 knots, then we go 60 nm forward in that same hour. Thus, we can draw a right triangle of length 60 with a perpendicular vector of length x. Applying the 60:1 rule, we know that our wind correction angle is simply x degrees. Now let's say we're doing 120 kts. That means that we go 120 nm in an hour while drifting x nm. In the time we go 60 nm, we drift x/2 nm. Generalizing this gives us WCA = (60 / TAS) * x. The faster we go, the smaller that wind correction gets. This rule starts to fall apart when our WCA gets above 20 degrees, but it mostly works. For those of you keeping score, it's basically an observation that θ and tan(θ) scale roughly linearly when angles are small.
Vertical Descent points
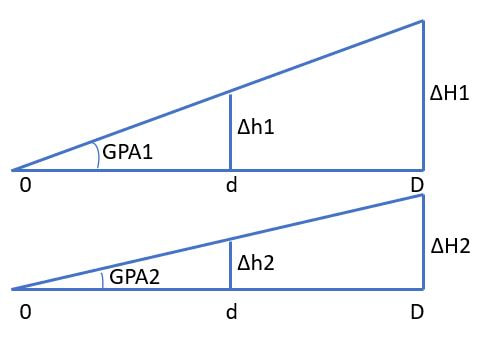
Some charts don't tell you how far away from the runway you should expect to break out of the soup if you're flying a proper CDFA. To calculate how far back we ought to be at this visual descent point, we need to know some reference points, our descent gradient, and the height to lose. We know that GPA degrees = 100 (GPA) ft/nm, and that as the vertical distance increases for a given GPA, so must the lateral distance, at the same rate. In other words, the relationship between ∆h1/d is the same as ∆H1/D. Looking at the two triangles sketched out, we also see that a shallower angle gives a smaller ∆h. This means that our equation for Dvdp will need to have ∆h in the numerator and GPA in the denominator. Our units for ∆h are usually feet, our GPAs are usually degrees, and the distances we want are in nm. Thus we need to use our gradient substitution and we get the following:
Dvdp nm = ∆h ft / (GPA * 100) ft/nm
Dvdp nm = ∆h ft / (GPA * 100) ft/nm
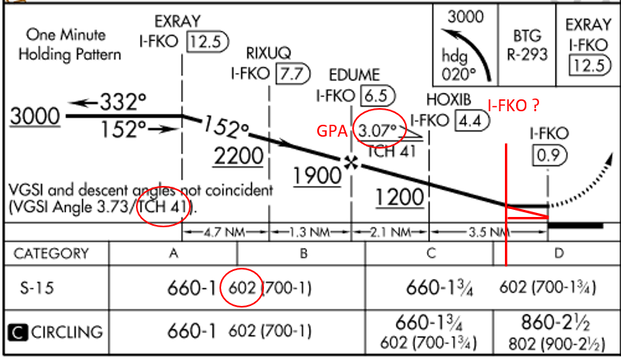
When we divide those out, the feet in the numerator cancel the ft/nm in the denominator and leaves us with nm as our output, which is exactly what we were looking for. Let's apply this to a scenario to help it stick. Let's look at the Scappoose Localizer 15. The red vertical line represents where we should break out. First, we need to find ∆h. In this case, the MAP is at the threshold. If we want to draw a triangle back from there, we need to account for the TCH in our calculations. We have the S-15 mins at 602 AGL, so we know that ∆h = mins AGL - TCH = 602 - 41 = 561. Our GPA is 3.07 degrees, which we multiply by 100 to get a gradient of 307 ft/nm. Putting this all together gives us this:
Dvdp nm = ∆h ft / (GPA * 100) ft/nm = 561 ft / 307 ft/nm = 1.83 nm.
Let's round that off to the nearest .1 nm and call it 1.8 nm. For those insistent on doing it trigonometrically, 561 / tan(3.07) = 10460 ft, which is 1.72 nm. Close enough....
We're not done yet! If we want to figure out I-FKO ? we need to account for the fact that the threshold is actually at I-FKO .9, so we need to add that into our 1.8 nm to give us I-FKO 2.7 for our VDP. The most important part of the process is sketching out the triangles and ensuring that your units are well labeled. If you don't account for TCH in ∆h, you might draw a longer triangle that would put you on brick one instead of the captain bars (where you ought to be) and consequently be low on profile. Small errors in height with shallow angles will result in big errors on distance, so it's important to get that right.
Dvdp nm = ∆h ft / (GPA * 100) ft/nm = 561 ft / 307 ft/nm = 1.83 nm.
Let's round that off to the nearest .1 nm and call it 1.8 nm. For those insistent on doing it trigonometrically, 561 / tan(3.07) = 10460 ft, which is 1.72 nm. Close enough....
We're not done yet! If we want to figure out I-FKO ? we need to account for the fact that the threshold is actually at I-FKO .9, so we need to add that into our 1.8 nm to give us I-FKO 2.7 for our VDP. The most important part of the process is sketching out the triangles and ensuring that your units are well labeled. If you don't account for TCH in ∆h, you might draw a longer triangle that would put you on brick one instead of the captain bars (where you ought to be) and consequently be low on profile. Small errors in height with shallow angles will result in big errors on distance, so it's important to get that right.
Turning inbound from an arc
Turning in from an arc is a special application of the rule with a simplified equation. More here including a proof.
Outbound points in a hold
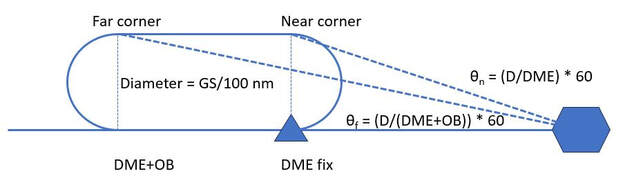
Let's say you're holding somewhere on a DME fix and you want to know which radial you should be on when you're outbound. This is helpful if you're an instrument student practicing unpublished holds in the sim and your instructor fails a bunch of equipment on you to force you to fly the green needles and not the pink ones (I like to do that...). We know that the turn radius is just GS/200, so the diameter of our holding pattern should be D=GS/100. If we're flying small airplanes at 100 knots, that's convenient because we can use D=1 nm. Given our DME and turn diameter we can find θ. We know that tan(θ)=θ/60, so a bit of algebra:
Multiply both sides by 60 and rearrange:
θ = tan(θ) * 60
tan(θ) at the near corner is D/DME. At the far corner, it's D/DME+OB, where OB is the outbound leg length. Thus θ=(D/DME)*60. Say you're flying along at 100 knots in a 6 DME hold, then D = 1 nm, tan(θ) = 1/6, which we then multiply by 60 to get θ = 60/6 = 10 degrees. In the far corner we're looking at about 7.5 nm, so θ = (1/7.5) * 60 = 8 degrees. If you're using a bearing pointer, you can see how the angles change and use it to make corrections to better anticipate when to turn. If you're flying the hold no-gyros without too much crosswind and the DME fix is far enough out that θ is only a few degrees, then you might want to consider twisting the outbound course to the outbound + θ number and track the needle on the outbound leg if it's more accurate than guessing with the mag compass. Use all the tools you have.
Multiply both sides by 60 and rearrange:
θ = tan(θ) * 60
tan(θ) at the near corner is D/DME. At the far corner, it's D/DME+OB, where OB is the outbound leg length. Thus θ=(D/DME)*60. Say you're flying along at 100 knots in a 6 DME hold, then D = 1 nm, tan(θ) = 1/6, which we then multiply by 60 to get θ = 60/6 = 10 degrees. In the far corner we're looking at about 7.5 nm, so θ = (1/7.5) * 60 = 8 degrees. If you're using a bearing pointer, you can see how the angles change and use it to make corrections to better anticipate when to turn. If you're flying the hold no-gyros without too much crosswind and the DME fix is far enough out that θ is only a few degrees, then you might want to consider twisting the outbound course to the outbound + θ number and track the needle on the outbound leg if it's more accurate than guessing with the mag compass. Use all the tools you have.
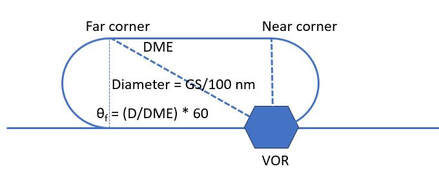
If you're holding on the VOR on a timed leg doing standard-rate turns, then your diameter and outbound leg length will scale at the same rate. In a 1-minute hold at 100 kts, you'll have a 1 nm diameter and a far corner at 1.667 nm and a DME of 1.94. Applying the rule would get us θ = 36, but at these big angles the rule falls apart a bit.
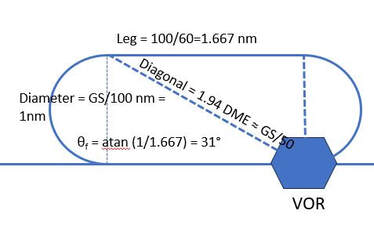
If instead we solved it trigonometrically, we get θ=atan(1/1.667)=30.96 degrees, which is close to 30. This means that when you're at the far corner, you should be about 30 radials from the outbound course and about GS/50 DME from the VOR. In a situation where you're partial panel and using the bearing pointer, this 30-degree reference will give you useful clues as to whether to tighten or widen your turn inbound to get onto the inbound course.