Density for Dummies
If, like me, you were a student pilot who disliked spinning whiz wheels and doing paper nav logs for CAS/TAS conversons, you might consider it worth the investment of time to understand some physics and density computations so that you can get your computer to do it for you. In the process, you'll gain enough knowledge of how it actually works to explain it satisfactorily on a checkride, or at least bamboozle your evaluator into giving up that line of questioning.
As we learned in the basic lift explanation, lift scales linearly with density, and quadratically with TAS. Our airplanes "feel" the air as CAS, and we use IAS as a proxy. In practice, we usually fly our maneuvers at a given IAS, which means we expect the plane to give us a constant lift output at that speed. Whenever we want to know how fast we're actually going through the airmass, say to compute time or a climb gradient, then we need to convert CAS to TAS. If we hold lift constant, we need to mess with the other variables:
L= ½ CL * S * ρ * α * v^2
If we want to correct CAS to TAS, then we can freeze the values for CL, S, and α to get the interplay between ρ and v^2. Thus we get:
L = ρ * v^2
If we want to baseline L=1 (an arbitrary value), then we get
1 = ρ * v^2
Rearranging this gets us
1/ρ = v^2
Taking the square root of both sides
1/√ρ = v
In other words, for a given amount of lift, TAS scales as the inverse square root of density. If we're working in an iso-lift world (i.e. constant CAS), then we can substitute that in for our arbitrary lift target and say
CAS/√ρ = TAS
Now that we have our equation, we need to figure out how ρ changes with different parameters, which will require some elementary physics. The ideal gas law states that the "relation between the pressure P, volume V, and temperature T of a gas in the limit of low pressures and high temperatures, such that the molecules of the gas move almost independently of each other. In such a case, all gases obey an equation of state known as the ideal gas law: PV = nRT, where n is the number of moles of the gas and R is the universal (or perfect) gas constant, 8.31446261815324 joules per kelvin per mole." We care about density, or the number of moles in a given volume, i.e. n/V. Rearranging the equation:
PV = nRT
PV/RT = n
P/RT = n/V
That equal number of molecules per unit volume is just density, ρ. R is just a constant, so as long as we use ratios of other numbers, we can leave it off. In other words:
ρ=P/T
To fly airplanes, we typically want to know how ρ changes, ∆ρ. We know that it scales linearly with pressure, and inversely with temperature, so all we need to do is plug those values in so that we can solve the below:
∆ρ=∆P/∆T
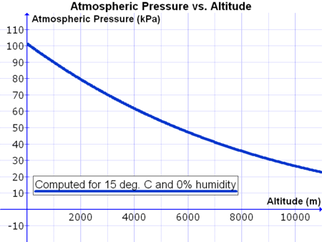
We have a construct for the standard atmosphere, ISA, which stipulates that P0=29.92 in Hg (or 1013 HPa) and T0=15 degrees C. Our default values for ρ, ρ0, is 1.225 kg/m^3. What we're after for our computations is the ratio of ρ/ρ0, also known as σ ("sigma"). We'll need to convert the T to Kelvin, so add 273.15 to the values of C to get T0=288.15K. Then we need to use our actual values for P and T to figure out the density change. Thus we end up with this:
ρ/ρ0 = σ = [(P/P0) * (T0/T)]
σ = [(P/29.92) * (288.15/T)]
Take a sample pressure of P=28.00. As P decreases in the numerator, ρ and σ decrease as well (by 28.00/29.92). If we take a warmer-than-standard temperature, T=300K, and plug that in on the right side, then 288.15/300 is less than 1, so our density goes down. Ok, looks like we got it right. Now we can punch in any values for pressure and temperature to get our offsets. Taking those sample values gives us this:
σ = (28.00/29.92) * (288.15/300) = .90
In other words, with those pressure and temperature values, we have 90% the density that we normally have under ISA SL conditions. If we wanted to use that for an airspeed conversion, we could plug it in here:
CAS/√σ = TAS
100/√.90 = 105.5 KTAS
As we learned in the basic lift explanation, lift scales linearly with density, and quadratically with TAS. Our airplanes "feel" the air as CAS, and we use IAS as a proxy. In practice, we usually fly our maneuvers at a given IAS, which means we expect the plane to give us a constant lift output at that speed. Whenever we want to know how fast we're actually going through the airmass, say to compute time or a climb gradient, then we need to convert CAS to TAS. If we hold lift constant, we need to mess with the other variables:
L= ½ CL * S * ρ * α * v^2
If we want to correct CAS to TAS, then we can freeze the values for CL, S, and α to get the interplay between ρ and v^2. Thus we get:
L = ρ * v^2
If we want to baseline L=1 (an arbitrary value), then we get
1 = ρ * v^2
Rearranging this gets us
1/ρ = v^2
Taking the square root of both sides
1/√ρ = v
In other words, for a given amount of lift, TAS scales as the inverse square root of density. If we're working in an iso-lift world (i.e. constant CAS), then we can substitute that in for our arbitrary lift target and say
CAS/√ρ = TAS
Now that we have our equation, we need to figure out how ρ changes with different parameters, which will require some elementary physics. The ideal gas law states that the "relation between the pressure P, volume V, and temperature T of a gas in the limit of low pressures and high temperatures, such that the molecules of the gas move almost independently of each other. In such a case, all gases obey an equation of state known as the ideal gas law: PV = nRT, where n is the number of moles of the gas and R is the universal (or perfect) gas constant, 8.31446261815324 joules per kelvin per mole." We care about density, or the number of moles in a given volume, i.e. n/V. Rearranging the equation:
PV = nRT
PV/RT = n
P/RT = n/V
That equal number of molecules per unit volume is just density, ρ. R is just a constant, so as long as we use ratios of other numbers, we can leave it off. In other words:
ρ=P/T
To fly airplanes, we typically want to know how ρ changes, ∆ρ. We know that it scales linearly with pressure, and inversely with temperature, so all we need to do is plug those values in so that we can solve the below:
∆ρ=∆P/∆T
We have a construct for the standard atmosphere, ISA, which stipulates that P0=29.92 in Hg (or 1013 HPa) and T0=15 degrees C. Our default values for ρ, ρ0, is 1.225 kg/m^3. What we're after for our computations is the ratio of ρ/ρ0, also known as σ ("sigma"). We'll need to convert the T to Kelvin, so add 273.15 to the values of C to get T0=288.15K. Then we need to use our actual values for P and T to figure out the density change. Thus we end up with this:
ρ/ρ0 = σ = [(P/P0) * (T0/T)]
σ = [(P/29.92) * (288.15/T)]
Take a sample pressure of P=28.00. As P decreases in the numerator, ρ and σ decrease as well (by 28.00/29.92). If we take a warmer-than-standard temperature, T=300K, and plug that in on the right side, then 288.15/300 is less than 1, so our density goes down. Ok, looks like we got it right. Now we can punch in any values for pressure and temperature to get our offsets. Taking those sample values gives us this:
σ = (28.00/29.92) * (288.15/300) = .90
In other words, with those pressure and temperature values, we have 90% the density that we normally have under ISA SL conditions. If we wanted to use that for an airspeed conversion, we could plug it in here:
CAS/√σ = TAS
100/√.90 = 105.5 KTAS
Rules of THumb
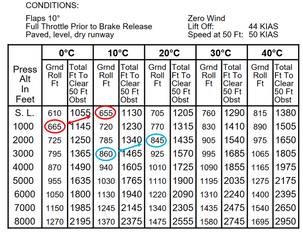Cessna 172 POH illustrating similar trade of 1k feet per 10 degrees
Now that we know how all of this fits together, let's apply it to come common scenarios to see how we can make it work quickly.
Pressure changes with altitude at about 1 in Hg / 1000 feet in the lower atmosphere. Thus at 1000 ft:
P/P0=28.92/29.92, or roughly 29/30, or .97. This means that we have 3% ∆ρ/ in Hg or per 1000 ft.
Take an example of temperature being 1 degree warmer than standard. T0/T = 288.15/289.15 = .997, or a .3% ∆ρ. The intuition here is that 288 is close to 300, so a 1-degree (C or K) change in temperature at 300 degrees will get you a third of a percent ∆ρ.
Combining those two rules above: 10 degrees ∆T is equivalent to 1 in Hg ∆P at low levels near ISA SL. If you look in your plane's POH, you'll probably see this relationship in the performance tables.
Pressure changes with altitude at about 1 in Hg / 1000 feet in the lower atmosphere. Thus at 1000 ft:
P/P0=28.92/29.92, or roughly 29/30, or .97. This means that we have 3% ∆ρ/ in Hg or per 1000 ft.
Take an example of temperature being 1 degree warmer than standard. T0/T = 288.15/289.15 = .997, or a .3% ∆ρ. The intuition here is that 288 is close to 300, so a 1-degree (C or K) change in temperature at 300 degrees will get you a third of a percent ∆ρ.
Combining those two rules above: 10 degrees ∆T is equivalent to 1 in Hg ∆P at low levels near ISA SL. If you look in your plane's POH, you'll probably see this relationship in the performance tables.
CAS/TAS conversions: for values of σ near 1, taking the square root gets you about halfway between σ and 1. For example: if σ=.9, √.9=.95. Plugging this into our above rules, we get a 1.5% increase in TAS per 1000 feet or per 10 degrees warmer.
The knowledge about σ and √σ is easier to work with, because you can easily relate what happens with your airplane. If I asked you how your TAS would be different from ISA SL where σ=1 versus at a DA of 3200 feet, you'd probably be a lot more stuck than with σ=.9.
If you do get forced to use the density altitude abstraction instead of our favorite Greek letters, you need to be a bit more careful. We earlier derived the fact that you trade about 1000 feet for 10 degrees at constant density, but the ISA atmosphere cools 2 degrees per thousand with altitude due to adiabatic lapse. Thus, to get the equivalent value for σ from +1000 feet and -2 degrees under ISA just by changing temperature, we need to make both halves of the equation equal and solve for our new T. In this scenario, we'll also be using the ISA pressure for 1000 feet (more on that below):
σ = (28.85/29.92)*(288.15/286.15) = .971 = (29.92/29.92*(288.15/T)
.971 = 288.15/T
.971/288.15 = T
T = 296.56K = 23.41C
23.41C is 8.41 degrees warmer than 15, so to get ∆DA/degree we simply divide 1000/8.41 = 118.9, or round it and say 120 feet DA per degree. Napkin math supports this as well: with +1000 and -2 degrees we trade the isothermal density of 8 degrees, and 1000/8 gives us 120ish. Just be careful about when to add and subtract, make sure you sanity check the output.
The knowledge about σ and √σ is easier to work with, because you can easily relate what happens with your airplane. If I asked you how your TAS would be different from ISA SL where σ=1 versus at a DA of 3200 feet, you'd probably be a lot more stuck than with σ=.9.
If you do get forced to use the density altitude abstraction instead of our favorite Greek letters, you need to be a bit more careful. We earlier derived the fact that you trade about 1000 feet for 10 degrees at constant density, but the ISA atmosphere cools 2 degrees per thousand with altitude due to adiabatic lapse. Thus, to get the equivalent value for σ from +1000 feet and -2 degrees under ISA just by changing temperature, we need to make both halves of the equation equal and solve for our new T. In this scenario, we'll also be using the ISA pressure for 1000 feet (more on that below):
σ = (28.85/29.92)*(288.15/286.15) = .971 = (29.92/29.92*(288.15/T)
.971 = 288.15/T
.971/288.15 = T
T = 296.56K = 23.41C
23.41C is 8.41 degrees warmer than 15, so to get ∆DA/degree we simply divide 1000/8.41 = 118.9, or round it and say 120 feet DA per degree. Napkin math supports this as well: with +1000 and -2 degrees we trade the isothermal density of 8 degrees, and 1000/8 gives us 120ish. Just be careful about when to add and subtract, make sure you sanity check the output.
Making the computers do it for us
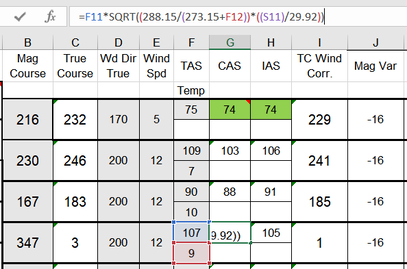
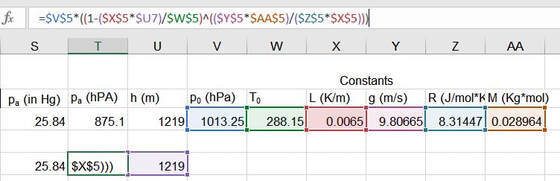
Applying this to nav log scenarios like climb gradients and TAS conversions is pretty easy. Simply enter your planned altitudes and the temperatures that will be at those altitudes into a spreadsheet. Then calculate the value for σ with those:
σ=[(<actual pressure at altitude>/29.92) * (288.15/<actual temperature at altitude>)]
If you're using HPa, replace the 29.92 with 1013.25
For lower altitudes, you can use the approximation that the pressure lapse rate is 1 in Hg per 1000 ft. This approximation falls apart the higher you go. Think about it this way: imagine you stack a pile of compressible items like sponges on top of one another. The ones lower in the stack will get squeezed together by the weight of the ones above them. Now imagine you stack 30 sponges, each one representing one inch of Mercury in pressure. If you measure the compressed ones at the bottom, they might have a thickness of, let's say, 1 inch. The further up the stack you go, the less compression from overlying sponges you get, so the thickness of the sponges will expand past 1 inch. The higher you go, the greater the thickness of the sponge. This same concept applies to the air in the atmosphere: lower parcels of air have a steeper pressure gradient than higher ones for the same reason, so an assumption of a linear pressure lapse of 1 in Hg/1k ft only works for the first few thousand feet.
σ=[(<actual pressure at altitude>/29.92) * (288.15/<actual temperature at altitude>)]
If you're using HPa, replace the 29.92 with 1013.25
For lower altitudes, you can use the approximation that the pressure lapse rate is 1 in Hg per 1000 ft. This approximation falls apart the higher you go. Think about it this way: imagine you stack a pile of compressible items like sponges on top of one another. The ones lower in the stack will get squeezed together by the weight of the ones above them. Now imagine you stack 30 sponges, each one representing one inch of Mercury in pressure. If you measure the compressed ones at the bottom, they might have a thickness of, let's say, 1 inch. The further up the stack you go, the less compression from overlying sponges you get, so the thickness of the sponges will expand past 1 inch. The higher you go, the greater the thickness of the sponge. This same concept applies to the air in the atmosphere: lower parcels of air have a steeper pressure gradient than higher ones for the same reason, so an assumption of a linear pressure lapse of 1 in Hg/1k ft only works for the first few thousand feet.
|
If you want to be a bit more precise and have your nav logs work better, you should use the ISA atmospheric pressure equation:
P=P0 * (1-L*h)/T0)^[(g*M)/(R0*L)]. That looks really ugly, but the good news is that you only need to set it up once to get your pressure outputs. In my template, I just converted feet to meters, then used the formula to get the HPa answer for pressure, and converted it back to In Hg. If you're using HPa anyway, you can skip the last step. |
|
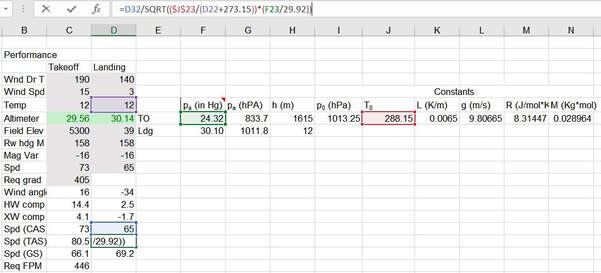
You can apply the same correction to takeoff performance calculations as well. Grab your METAR and field elevation, take the cosine of your wind angle times speed to get your headwind component, convert your CAS to TAS, apply the wind to your TAS to get GS, and then multiply GS/60 with your DP's gradient to get your required FPM:
A word of caution: whenever you ask a computer to do anything, it will suffer from the GIGO principle, so I recommend checking your outputs. I almost got into hot water on a checkride when I entered an altimeter setting of "3005" and not "30.05" as I should have done. The TAS was an absurdly low number, as one would expect when flying through dense molasses. Fortunately I caught it before my examiner did and changed it, then put a cell highlight in place to block values below 28.00 or above 31.50, and green highlight cell values in the middle. I highly recommend hiding those pressure lapse calculation columns as well, that's a rabbit hole I would not want to go down on a checkride.
Applying all of these, you should be able to have your computer do your CAS/TAS conversions more quickly, as well as estimate some practical implications of density changes on the fly using those rules of thumb. Lastly, if all of this made sense, it should make you more proficient at performing and explaining density corrections and airspeed when you do get evaluated. In my experience, an evaluator's interest scales inversely with the number of Greek letters you put in a sentence. As an old mentor of mine once said, "If you can't wow them with your wisdom, baffle them with your bullshit."
Applying all of these, you should be able to have your computer do your CAS/TAS conversions more quickly, as well as estimate some practical implications of density changes on the fly using those rules of thumb. Lastly, if all of this made sense, it should make you more proficient at performing and explaining density corrections and airspeed when you do get evaluated. In my experience, an evaluator's interest scales inversely with the number of Greek letters you put in a sentence. As an old mentor of mine once said, "If you can't wow them with your wisdom, baffle them with your bullshit."
A note on the oft-maligned whiz wheel
When I first learned to use the whiz wheel, it was a rote process of applying a rule and looking for the outputs without considering how they came to be. Truly understanding density helped me appreciate the genius of the device. If you look closely at the gradations on the temperature scale, you'll notice that the high temperatures are clustered more closely. This is because as the values of T increase, a one-degree change becomes a smaller overall fraction. You'll also notice that the pressure altitude spacing gets progressively wider, but not quite as fast as you might expect. That's because the alignment of those numbers gives us √σ, which we use to do our TAS/CAS on the outer ring. To compensate for the √σ on the DA scale (where we'd need σ), that one likewise has greater spacing to account for the correction. Pretty genius.