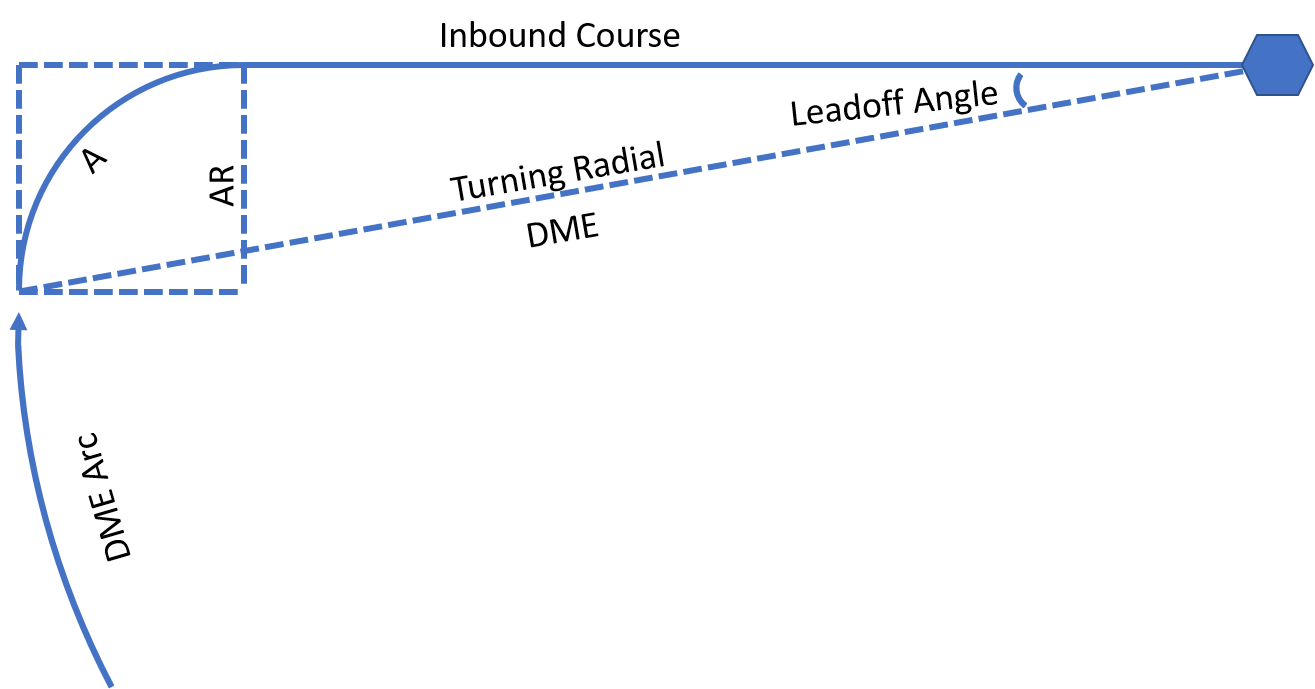
Turning inbound from an Arc
The first time I flew an arc approach in the simulator during my instrument training, we tried the VOR-A into Paine Field, and my approach ground track looked something like this:
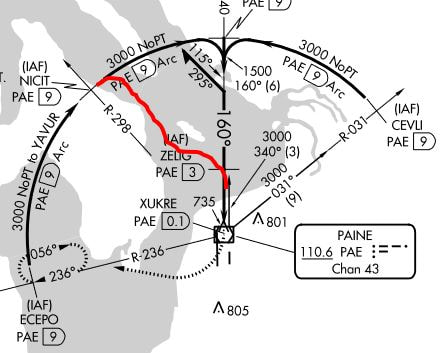
I told myself, and my amused CFII, that I wouldn't do that again, and that there must be a better way to turn inbound on that arc, and set about figuring out what that would look like. I sketched it out a bit to look like this:
The goal is to find the leadoff angle (LA), and from that derive the turning radial to roll out right on center. We already know about the relationship between our ground speed and the turn-in arc flown and the radius of that arc, so we can use that go get started. Looking at that little box on the left, we have a nice right triangle of base DME and height AR. Thus, the tangent of LA is AR/DME, or LA=atan(AR/DME). All we now need to do is whip out our calculator when we're in the soup and punch in LA=atan[(GS/188)/DME], no pressure. Don't forget to make sure it's not in radians mode. Maybe a bit of turbulence will help you fat-finger it and send you off course, just make sure cumulus granitus isn't nearby when losing situational awareness.
We obviously don't want to be fiddling with calculators in flight, so let's make up a rule that will work to approximate this. Because AR scales linearly with GS, and DME affects LA, I figured it had to be some function of GS/DME. I tried a few combinations and came up with the following:
Rule: LA=GS/3*DME
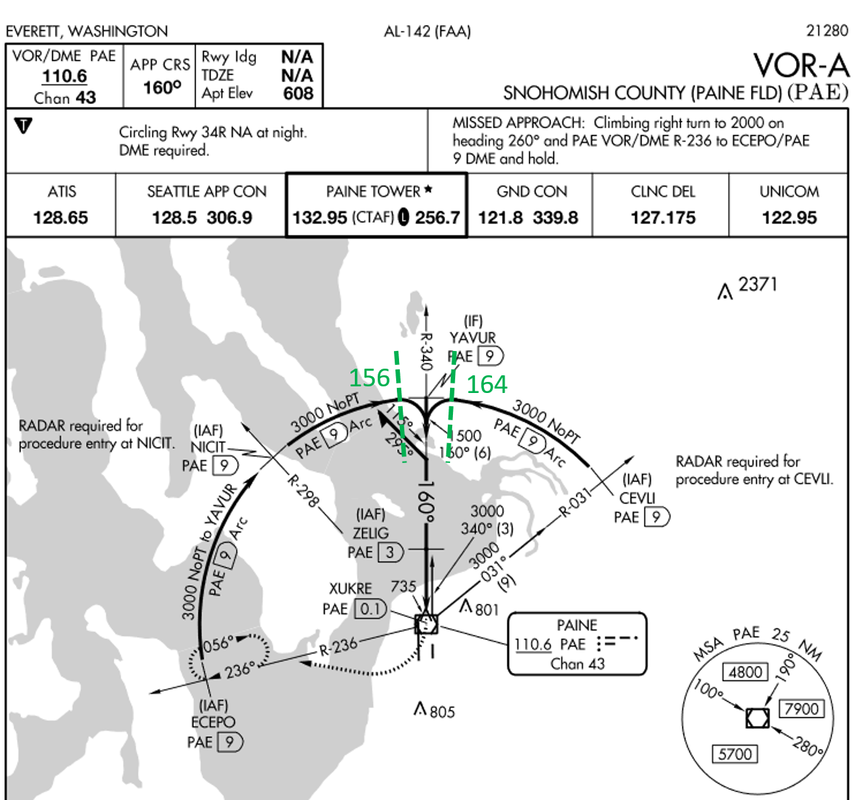
This works when the angles are fairly small, which they usually are. Applying this to the example of the Paine VOR-A approach flown at 100 kts:
Trig: LA=atan[(100/188)/9]=3.38 degrees
Rule: LA=100/(3*9)=3.7 degrees
The rule gives you an answer that's about 10% too aggressive which is mostly trivial in a world where our instruments only go to full degrees. If you're on a small arc like 5 DME and you're doing 150 knots, it'll be a full degree early, but you can roll out a tad slowly and nobody would be any the wiser.
The next time I flew the VOR-A with my instructor, I told him about the rule and set the CDI to 156 degrees. As soon as we crossed the radial I started the turn, then adjusted the CDI to the 160 inbound, and rolled out right on the needle. Now that I've started teaching it myself, I tell learners to pre-calculate the turn-in radials and scribble them on the plate to make life easier for themselves:
We obviously don't want to be fiddling with calculators in flight, so let's make up a rule that will work to approximate this. Because AR scales linearly with GS, and DME affects LA, I figured it had to be some function of GS/DME. I tried a few combinations and came up with the following:
Rule: LA=GS/3*DME
This works when the angles are fairly small, which they usually are. Applying this to the example of the Paine VOR-A approach flown at 100 kts:
Trig: LA=atan[(100/188)/9]=3.38 degrees
Rule: LA=100/(3*9)=3.7 degrees
The rule gives you an answer that's about 10% too aggressive which is mostly trivial in a world where our instruments only go to full degrees. If you're on a small arc like 5 DME and you're doing 150 knots, it'll be a full degree early, but you can roll out a tad slowly and nobody would be any the wiser.
The next time I flew the VOR-A with my instructor, I told him about the rule and set the CDI to 156 degrees. As soon as we crossed the radial I started the turn, then adjusted the CDI to the 160 inbound, and rolled out right on the needle. Now that I've started teaching it myself, I tell learners to pre-calculate the turn-in radials and scribble them on the plate to make life easier for themselves:
A colleague challenged me to solve the problem if we don't have a ground speed readout, so I went back to the whiteboard. We already know that AR=.64A and that we need 30 seconds in the turn. .64 is close to 2/3, so we can approximate that the radials we'll cover in 20 seconds is the same that we'll cover in the 30-second inbound turn. Thus, as we get close to our turn, we can center our needle and set a timer for 20 seconds, then measure the angular deflection. That's how far we need to lead the inbound turn. Example: we want to fly inbound on the 160 radial to PAE, and we're currently going through 140 inbound on our CDI. We center it and count 20 seconds, at which point it's drifted 4 degrees, meaning we're on 144 inbound. We now know it's a 4-degree leadoff, so we can twist the lead-in radial to 156 and roll out on 160.